| Issue |
EPL
Volume 133, Number 5, March 2021
|
|
|---|---|---|
| Article Number | 50005 | |
| Number of page(s) | 7 | |
| Section | General | |
| DOI | https://doi.org/10.1209/0295-5075/133/50005 | |
| Published online | 10 May 2021 | |
An overview of generalized entropic forms(a)
1 Mathematical Institute of the Serbian Academy of Sciences and Arts - Kneza Mihaila 36, 11000 Beograd, Serbia
2 Section for Science of Complex Systems, CeMSIIS, Medical University of Vienna - Vienna, Austria
3 Complexity Science Hub Vienna - Josefstädterstrasse 39, 1080 Vienna, Austria
4 Faculty of Nuclear Sciences and Physical Engineering, Czech Technical University in Prague - Břehová 7, 115 19 Prague, Czech Republic
5 Department of Physics, Ramakrishna Mission Vivekananda Educational and Research Institute - Belur Math, India
6 Istituto dei Sistemi Complessi, Consiglio Nazionale delle Ricerche, c/o Dipartimento di Scienza Applicata e Tecnologia del Politecnico di Torino - Corso Duca degli Abruzzi 24, 10129 Torino, Italy
Received: 4 December 2020
Accepted: 19 February 2021
The aim of this focus article is to present a comprehensive classification of the main entropic forms introduced in the last fifty years in the framework of statistical physics and information theory. Most of them can be grouped into three families, characterized by two-deformation parameters, introduced respectively by Sharma, Taneja, and Mittal (entropies of degree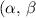 
)), by Sharma and Mittal (entropies of order 
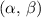), and by Hanel and Thurner (entropies of class 
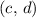). Many entropic forms examined will be characterized systematically by means of important concepts such as their axiomatic foundations à la Shannon-Khinchin and the consequent composability rule for statistically independent systems. Other critical aspects related to the Lesche stability of information measures and their consistency with the Shore-Johnson axioms will be briefly discussed on a general ground.
PACS: 05.20.-y – Classical statistical mechanics / 89.70.-a – Information and communication theory / 05.90.+m – Other topics in statistical physics, thermodynamics, and nonlinear dynamical systems (restricted to new topics in section 05)
© 2021 EPLA
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.