| Issue |
EPL
Volume 133, Number 5, March 2021
|
|
|---|---|---|
| Article Number | 57004 | |
| Number of page(s) | 7 | |
| Section | Condensed Matter: Electronic Structure, Electrical, Magnetic and Optical Properties | |
| DOI | https://doi.org/10.1209/0295-5075/133/57004 | |
| Published online | 06 April 2021 | |
Self-consistent harmonic approximation in presence of non-local couplings(a)
1 SISSA and INFN, Sezione di Trieste - Via Bonomea 265, I-34136 Trieste, Italy
2 Institute for Theoretical Physics, ETH Zürich - Wolfgang-Pauli-Str. 27, 8093 Zurich, Switzerland
3 Department of Physics, University of Trieste - Strada Costiera 11, I-34151 Trieste, Italy
4 Istituto dei Sistemi Complessi, Consiglio Nazionale delle Ricerche - Via Madonna del Piano 10, I-50019 Sesto Fiorentino, Italy
Received: 3 December 2020
Accepted: 12 February 2021
We derive the self-consistent harmonic approximation for the 2D XY model with non-local interactions. The resulting equation for the variational couplings holds for any form of the spin-spin coupling as well as for any dimension. Our analysis is then specialized to power-law couplings decaying with the distance r as 
in order to investigate the robustness, at finite σ, of the Berezinskii-Kosterlitz-Thouless (BKT) transition, which occurs in the short-range limit 
. We propose an ansatz for the functional form of the variational couplings and show that for any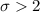 
the BKT mechanism occurs. The present investigation provides an upper bound 
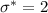for the critical threshold 
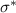above which the traditional BKT transition persists in spite of the non-local nature of the couplings.
PACS: 75.30.Kz – Magnetic phase boundaries (including classical and quantum magnetic transitions, metamagnetism, etc.) / 05.70.Fh – Phase transitions: general studies
© 2021 EPLA
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.