| Issue |
Europhys. Lett.
Volume 38, Number 5, May II 1997
|
|
|---|---|---|
| Page(s) | 323 - 328 | |
| Section | General | |
| DOI | https://doi.org/10.1209/epl/i1997-00246-4 | |
| Published online | 01 September 2002 | |
The relevance of Pólya's random-walk problem for the single-species reaction-diffusion system
International Centre of Theoretical Physics, Condensed Matter Section, P.O.Box 586, 34100 Trieste, Italy
Theoretische Polymerphysik - Rheinstr. 12, D-79104 Freiburg, Germany
Received:
6
September
1996
Accepted:
8
April
1997
The diffusion-limited reactions 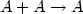 and
and  in dimension
d > 2 are reconsidered
from the point of view of the random-walk
theory.
It is pointed out that Pólya's theorem on the returning probability
of a random walker to the origin, which would imply a probability
less than one
for the meeting of two typical particles, would predict
the possibility of a state in which the reaction seems to
have spontaneously ceased, in contradiction with the very well
known asymptotic
in dimension
d > 2 are reconsidered
from the point of view of the random-walk
theory.
It is pointed out that Pólya's theorem on the returning probability
of a random walker to the origin, which would imply a probability
less than one
for the meeting of two typical particles, would predict
the possibility of a state in which the reaction seems to
have spontaneously ceased, in contradiction with the very well
known asymptotic  for the particles population of
these reactions.
In fact, a given condition is presented, in which
the relative particle number N(t)/N(0) decays to a
non-vanishing constant. The condition is that the
initial distribution of particles in the d-dimensional space has a
dimension γ, such that
for the particles population of
these reactions.
In fact, a given condition is presented, in which
the relative particle number N(t)/N(0) decays to a
non-vanishing constant. The condition is that the
initial distribution of particles in the d-dimensional space has a
dimension γ, such that  .
.
PACS: 05.40.+j – Fluctuation phenomena, random processes, and Brownian motion / 82.20.Mj – Nonequilibrium kinetics
© EDP Sciences, 1997
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


