| Issue |
EPL
Volume 133, Number 2, January 2021
|
|
|---|---|---|
| Article Number | 28001 | |
| Number of page(s) | 7 | |
| Section | Interdisciplinary Physics and Related Areas of Science and Technology | |
| DOI | https://doi.org/10.1209/0295-5075/133/28001 | |
| Published online | 23 March 2021 | |
Surface growth on tree-like lattices and the upper critical dimension of the KPZ class
Departamento de Física, Universidade Federal de Viçosa - 36570-900, Viçosa, MG, Brazil
(a) tiago@ufv.br
Received: 29 April 2020
Accepted: 11 December 2020
Aiming to investigate the upper critical dimension, du, of the KPZ class, in Saberi A. A., EPL, 103 (2013) 10005, some growth models were numerically analyzed using Cayley trees (CTs) as substrates, as a way to access their behavior in the infinite-dimensional limit, and some unexpected results were reported: logarithmic roughness scaling, differing for EW and KPZ models (indicating that even at 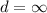 the KPZ nonlinearity is still relevant); beyond asymptotically rough EW surfaces above the upper critical dimension of the EW class. Motivated by these strange findings, I revisit these growth models here to show that such results are simple consequences of boundary effects, inherent to systems defined on CTs. In fact, I demonstrate that the anomalous boundary of the CT leads the growing surfaces to develop curved shapes, which explains the strange behaviors previously found for these systems, once the global “roughness” was analyzed for non-flat surfaces in the study above. Importantly, by measuring the height fluctuations at the central site of the CT, which can be seen as an approximation for the Bethe lattice, smooth surfaces are found for both EW and KPZ classes, consistently with the behavior expected for growing systems in dimensions
the KPZ nonlinearity is still relevant); beyond asymptotically rough EW surfaces above the upper critical dimension of the EW class. Motivated by these strange findings, I revisit these growth models here to show that such results are simple consequences of boundary effects, inherent to systems defined on CTs. In fact, I demonstrate that the anomalous boundary of the CT leads the growing surfaces to develop curved shapes, which explains the strange behaviors previously found for these systems, once the global “roughness” was analyzed for non-flat surfaces in the study above. Importantly, by measuring the height fluctuations at the central site of the CT, which can be seen as an approximation for the Bethe lattice, smooth surfaces are found for both EW and KPZ classes, consistently with the behavior expected for growing systems in dimensions 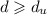 . Interesting features of the 1-point height fluctuations, such as the possibility of non-saturation in the steady state regime, are also discussed for substrates in general.
. Interesting features of the 1-point height fluctuations, such as the possibility of non-saturation in the steady state regime, are also discussed for substrates in general.
PACS: 81.15.Aa – Theory and models of film growth / 05.40.-a – Fluctuation phenomena, random processes, noise, and Brownian motion / 89.75.Da – Systems obeying scaling laws
© 2021 EPLA
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


