| Issue |
EPL
Volume 149, Number 6, March 2025
|
|
|---|---|---|
| Article Number | 62002 | |
| Number of page(s) | 6 | |
| Section | Mathematical and interdisciplinary physics | |
| DOI | https://doi.org/10.1209/0295-5075/adc0bb | |
| Published online | 07 April 2025 | |
Exact closed-form recurrence probabilities for biased random walks at any step number
Department of Physics, New York University - New York, NY, USA
Received: 26 September 2024
Accepted: 14 March 2025
We report on a closed-form expression for the survival probability of a discrete 1D biased random walk to not return to its origin after N steps. Our expression is exact for any N, including the elusive intermediate range, thereby allowing one to study its convergence to the large N limit. In that limit we recover Polyá's recurrence probability, i.e., the survival probability equals the magnitude of the bias. We then obtain a closed-form expression for the probability of last return. In contrast to the bimodal behavior for the unbiased case, we show that the probability of last return decays monotonically throughout the walk beyond a critical bias. We obtain a simple expression for the critical bias as a function of the walk length, and show that it saturates at 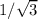 for infinitely long walks. This property is missed when using expressions developed for the large N limit. Finally, we discuss application to molecular motors’ biased random walks along microtubules, which are of intermediate step number.
for infinitely long walks. This property is missed when using expressions developed for the large N limit. Finally, we discuss application to molecular motors’ biased random walks along microtubules, which are of intermediate step number.
© 2025 EPLA. All rights, including for text and data mining, AI training, and similar technologies, are reserved
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


